관련 포스팅
Point-based Method: PointNet
개요이전 글 LiDAR에서 잠깐 언급했듯이 포인트 클라우드는 unordered한 irregular format으로 raw data 그대로 직접 딥러닝에 적용하기란 쉽지 않았다. Voxel grid나 이미지 집합으로 변환하여 사용하기에는
sohee-zoe.tistory.com
DGCNN: Dynamic Graph CNN for Learning on Point Clouds
Dynamic Graph CNN for Learning on Point Clouds
Abstract Point clouds provide a flexible and scalable geometric representation suitable for countless applications in computer graphics; they also comprise the raw output of most 3D data acquisition devices. Hence, the design of intelligent computational m
liuziwei7.github.io

Key Contributions
DGCNN은 PointNet과 Graph CNN를 결합한 네트워크로 포인트와 그 포인트에 인접한 포인트들의 관계를 설명하는 edge feature를 추출하는 `EdgeConv`라는 모듈을 제안한다. PointNet은 각 점들을 독립적으로 처리하여 permutation invariance를 유지하는 대신, 독립성으로 인해 점들 사이의 기하학적 관계를 무시하게 되어 local feature를 포착함에 있어 한계가 있다. DGCNN은 EdgeConv을 통해 local geometic structure 를 포착하면서도 permutation invariance를 유지할 수 있다. point간의 local graph를 구성하고 edge에 대한 embedding을 학습하여 유클리드 공간과 semantic 공간에서 모두 point를 그룹화할 수 있다. EdgeConv는 고정되어있지 않고 layer 간 그래프가 dynamic하게 업데이트되는 방식이다.
EdgeConv

Point Cloud
$ n $ 개의 points들로 이루어진 F-dimentional point cloud $ \mathbf X = \{ \mathbf x_i, ..., \mathbf x_n \} \subseteq \mathbb{R}^F $을 고려하자.
편의상 $ F = 3 $, 즉 3D point $ \mathbf x_i = (x_i, y_i, z_i) $ 라고 하자.
Graph

graph를 $\mathcal{G} = ( \mathcal{V, E} )$ 라고 할 때, $ \mathcal{V, E} $는 각각 vertices와 edges이다.
$ \mathcal{V} = \subset \mathbb{R}^c, \mathcal{E} = \subseteq \mathcal{V} \times \mathcal{V} $ 로 표현된다.
edge feature $ e_{ij} = h_{\Theta} ( \mathbf x_i, \mathbf x_j) $이고
$ h_\Theta : \mathbb{R}^F \times \mathbb{R}^F \to \mathbf{R}^{F'}$는 학습 가능한 파라미터인 $\Theta$ 집합을 갖는 nonlinear function이다.
다시 말해, $ h_\Theta $는 두 벡터 $ \mathbf x_i, \mathbf x_j $를 입력으로 받아 edge feature를 추출한다.
Edge Conv
그런 다음 각 vertex에서 나오는 edges와 관련된 edge features를 channel-wise symmetric aggregation operation $ \square $ (e.g., $ \sum $, max)을 적용하여 EdgeConv 연산을 정의한다.
최종적으로 $ i $-th vertex에서 EdgeConv 연산 결과는 다음과 같다.
$$ \mathbf x^{'}_{i} = \underset {j:(i,j) \in \mathcal{E}} \square h( \mathbf x_i, \mathbf x_j) $$
Choice of $ h $ and $ \square $
이제 $ \mathbf x_i $을 중심으로 주변의 점들 $ \{ \mathbf x_j : (i, j) \subseteq \mathcal{E} \} $로부터 $ \mathbf x^{'}_i $를 추출하기 위해 symmetric aggregation opration $ \square $과 edge feature를 추출하는 nonlinear function $ h_\Theta $을 선정해야 한다. 이를 선정하기 위한 과정은 다음과 같다.
1) standard convolution 사용
$$ x^{'}_{im} = \underset {j:(i,j) \in \mathcal{E}}{\sum} \mathbf \theta_m \cdot \mathbf x_j $$
구조적인 한계로 사용 불가능
2) PointNet 연산 활용
$$ h_\Theta (\mathbf x_i, \mathbf x_j) = h_\Theta (\mathbf x_i) $$
global shape information만 활용하는 한계 존재
3) Gaussian kernel과 pairwise distance 활용
$$ h_\Theta (\mathbf x_i, \mathbf x_j) = h_\Theta (\mathbf x_i), $$
$$ x^{'}_{im} = \underset {j \in \mathcal{V}}{\sum} ( h_{\theta(\mathbf x_j)} ) g(u(\mathbf x_i, \mathbf x_j)) $$
$ u $로 유클리드 공간에서 pairwise distance 계산하고 Gaussian kernel $ g $를 적용한 결과를 곱함
인접한 point에 대해 적용해서 local 정보는 잘 뽑지만 global structure는 잘 포착하지 못하는 한계 존재
4) 상대 거리를 입력으로 사용
$$ h_\Theta (\mathbf x_i, \mathbf x_j) = h_\Theta (\mathbf x_j - \mathbf x_i) $$
인접한 포인트와의 상대 거리를 이용하여 local feature를 잘 뽑아내지만, global 정보를 포착할 수 없는 한계 존재
5) asymmetric edge funtion: point $ \mathbf x_i $ 와 이웃 포인트의 상대 거리 $ \mathbf x_j - \mathbf x_i $를 모두 입력으로 사용
$$ h_\Theta (\mathbf x_i, \mathbf x_j) = \bar{h}_\Theta (\mathbf x_i, \mathbf x_j - \mathbf x_i) $$
절대적인 위치와 상대 거리 모두 사용하여 local, global feature를 모두 잘 포착
수식을 풀어서 쓰면,
절대적 위치 $ \mathbf x_i $와 상대적 거리 $ \mathbf x_j = \mathbf x_i $를 입력으로 받아 edge features를 추출하는 nonlinear funtion $ h_\Theta $ (MLP - ReLU)에 넣는다. 그런 다음 symmetric aggregation operation으로 max-pooling을 적용하여 최종 feature $ x^{'}_{im} $을 추출한다.
$$ e^{'}_{ijm} = \text{ReLU} ( \theta_m \cdot (\mathbf x_j - \mathbf x_i) + \phi_m \cdot \mathbf x_i ), $$
$$ \mathbf x^{'}_{im} = \underset {j:(i,j) \in \mathcal{E}}{\text {max}} e^{'}_{ijm} $$
$$ \text{where } \Theta = (\theta_1, ... \theta_M, \phi_1, ..., \phi_M) $$
Dynamic Graph Update
실험 결과 각 layer에서 생성된 feature space에서 최근접 이웃을 고려하는 k-NN을 사용하여 각 layer를 지날 때마다 graph를 재계산하면 효과적임을 제시한다.
아래 그림에서 볼 수 있듯이 layer를 거쳐갈수록 물리적인 거리보다 의미론적으로 유사한 점들에 더 연결 관계성을 보여 semantic segmentation을 잘해낸다는 점이다.
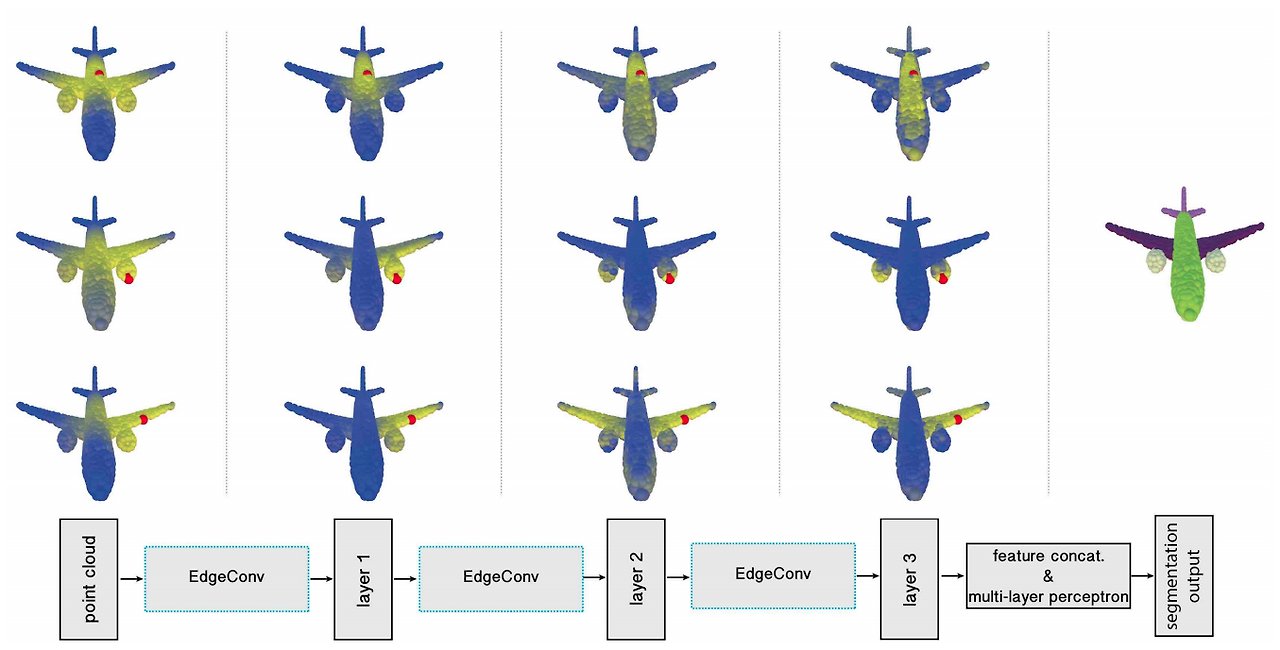
Evaluation





오래 되어서 자세히 기억은 안 나지만 DGCNN은 KNN으로 인해 계산 복잡도가 높고 graph를 계속 update하기 때문 PointNet보다 학습 시간이 2배 이상 걸렸던 거 같다. 당시 GPU 이슈도 있었어서 괴로웠던 기억밖에... 오랜만에 논문들을 다시 살펴보니 감회가 새롭기도 하다. 다음에 기회가 되면 PointPillars 논문 리뷰도 해보겠다.
'Spatial AI > SLAM' 카테고리의 다른 글
| 자율주행 오픈소스 데이터셋 & 소프트웨어 & 시뮬레이터 (0) | 2025.03.21 |
|---|---|
| 스마트 시티와 스마트 모빌리티 (0) | 2025.03.21 |
| Point-based Method: PointNet (0) | 2025.03.06 |
| LiDAR (Light Detection and Ranging) (0) | 2025.02.21 |
| RADAR (RAdio Detection And Ranging) (0) | 2025.02.19 |
